 |
|
An encoding of numbers so that adjacent numbers have a single digit differing
by 1. A binary Gray code
with 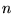 digits
corresponds to a Hamiltonian
path on an digits
corresponds to a Hamiltonian
path on an 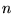 -D hypercube
(including direction reversals). The term Gray code is often used to
refer to a "reflected" code, or more specifically still, the binary
reflected Gray code. -D hypercube
(including direction reversals). The term Gray code is often used to
refer to a "reflected" code, or more specifically still, the binary
reflected Gray code.
To convert a binary number 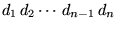 to its corresponding binary reflected Gray code, start at
the right with the digit to its corresponding binary reflected Gray code, start at
the right with the digit 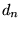 (the (the 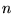 th, or last, digit). If the th, or last, digit). If the
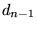 is 1, replace is 1, replace 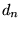 by by 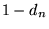 ; otherwise, leave it unchanged. Then proceed to ; otherwise, leave it unchanged. Then proceed to 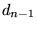 . Continue up to the first digit . Continue up to the first digit 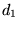 , which is kept the same since , which is kept the same since 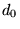 is assumed to be a 0. The resulting number is assumed to be a 0. The resulting number 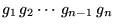 is the reflected binary Gray code. is the reflected binary Gray code.
To convert a binary reflected Gray code 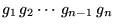 to a binary number,
start again with the to a binary number,
start again with the 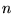 th digit, and compute th digit, and compute
If 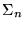 is 1, replace is 1, replace 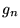 by by 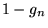 ; otherwise, leave it the unchanged. Next compute ; otherwise, leave it the unchanged. Next compute
and so on. The resulting number 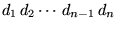 is the binary number
corresponding to the initial binary reflected Gray code. is the binary number
corresponding to the initial binary reflected Gray code.
The code is called reflected because it can be generated in the
following manner. Take the Gray code 0, 1. Write it forwards, then
backwards: 0, 1, 1, 0. Then append 0s to the first half and 1s to
the second half: 00, 01, 11, 10. Continuing, write 00, 01, 11, 10,
10, 11, 01, 00 to obtain: 000, 001, 011, 010, 110, 111, 101, 100,
... (Sloane's A014550). Each
iteration therefore doubles the number of codes. The Gray codes
corresponding to the first few nonnegative integers are given in the
following table.
| 0 |
0 |
20 |
11110 |
40 |
111100 |
| 1 |
1 |
21 |
11111 |
41 |
111101 |
| 2 |
11 |
22 |
11101 |
42 |
111111 |
| 3 |
10 |
23 |
11100 |
43 |
111110 |
| 4 |
110 |
24 |
10100 |
44 |
111010 |
| 5 |
111 |
25 |
10101 |
45 |
111011 |
| 6 |
101 |
26 |
10111 |
46 |
111001 |
| 7 |
100 |
27 |
10110 |
47 |
111000 |
| 8 |
1100 |
28 |
10010 |
48 |
101000 |
| 9 |
1101 |
29 |
10011 |
49 |
101001 |
| 10 |
1111 |
30 |
10001 |
50 |
101011 |
| 11 |
1110 |
31 |
10000 |
51 |
101010 |
| 12 |
1010 |
32 |
110000 |
52 |
101110 |
| 13 |
1011 |
33 |
110001 |
53 |
101111 |
| 14 |
1001 |
34 |
110011 |
54 |
101101 |
| 15 |
1000 |
35 |
110010 |
55 |
101100 |
| 16 |
11000 |
36 |
110110 |
56 |
100100 |
| 17 |
11001 |
37 |
110111 |
57 |
100101 |
| 18 |
11011 |
38 |
110101 |
58 |
100111 |
| 19 |
11010 |
39 |
110100 |
59 |
100110 |
The binary reflected Gray code is closely related to the
solutions of the towers of
Hanoi and baguenaudier,
as well as to Hamiltonian circuits of hypercube graphs (Skiena 1990,
p. 149).
 Baguenaudier,
Binary, Hilbert
Curve, Ryser
Formula, Thue-Morse
Sequence, Towers of
Hanoi Baguenaudier,
Binary, Hilbert
Curve, Ryser
Formula, Thue-Morse
Sequence, Towers of
Hanoi

References
Gardner, M. "The Binary Gray Code." Ch. 2 in Knotted Doughnuts and Other
Mathematical Entertainments. New York: W. H.
Freeman, 1986.
Gilbert, E. N. "Gray Codes and Paths on the 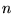 -Cube." Bell System Tech. J. 37, 815-826,
1958. -Cube." Bell System Tech. J. 37, 815-826,
1958.
Gray, F. "Pulse Code Communication." United States Patent Number
2,632,058. March 17, 1953.
Nijenhuis, A. and Wilf, H. Combinatorial Algorithms for
Computers and Calculators, 2nd ed. New York: Academic
Press, 1978.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.;
and Vetterling, W. T. "Gray Codes." §20.2 in Numerical Recipes in FORTRAN:
The Art of Scientific Computing, 2nd ed. Cambridge,
England: Cambridge University Press, pp. 886-888, 1992.
Skiena, S. "Gray Code." §1.5.3 in Implementing Discrete
Mathematics: Combinatorics and Graph Theory with
Mathematica. Reading, MA: Addison-Wesley,
pp. 42-43 and 149, 1990.
Sloane, N. J. A. Sequences A014550 in "An On-Line
Version of the Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/eisonline.html.
Vardi, I. Computational Recreations in
Mathematica. Redwood City, CA: Addison-Wesley,
pp. 111-112 and 246, 1991.
Wilf, H. S. Combinatorial Algorithms: An
Update. Philadelphia, PA: SIAM, 1989.
© 1996-2000 Eric W. Weisstein and Wolfram
Research, Inc.
Sponsored by Wolfram Research, Inc., makers of
Mathematica
|





