Digital Encoders
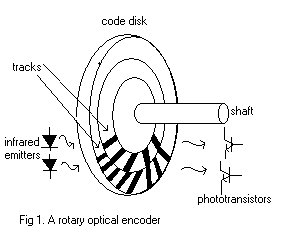 A digital optical encoder is a
device that converts motion into a sequence of digital pulses. By counting a
single bit or by decoding a set of bits, the pulses can be converted to relative
or absolute position measurements. Encoders have both linear and rotary
configurations, but the most common type is rotary. Rotary encoders are
manufactured in two basic forms: the absolute encoder where a unique digital
word corresponds to each rotational position of the shaft, and the incremental
encoder, which produces digital pulses as the shaft rotates, allowing
measurement of relative position of shaft. Most rotary encoders are composed of
a glass or plastic code disk with a photographically deposited radial pattern
organized in tracks. As radial lines in each track interrupt the beam between a
photoemitter-detector pair, digital pulses are produced.
A digital optical encoder is a
device that converts motion into a sequence of digital pulses. By counting a
single bit or by decoding a set of bits, the pulses can be converted to relative
or absolute position measurements. Encoders have both linear and rotary
configurations, but the most common type is rotary. Rotary encoders are
manufactured in two basic forms: the absolute encoder where a unique digital
word corresponds to each rotational position of the shaft, and the incremental
encoder, which produces digital pulses as the shaft rotates, allowing
measurement of relative position of shaft. Most rotary encoders are composed of
a glass or plastic code disk with a photographically deposited radial pattern
organized in tracks. As radial lines in each track interrupt the beam between a
photoemitter-detector pair, digital pulses are produced.
Absolute encoder
The optical disk of the absolute encoder is designed to produce a digital
word that distinguishes N distinct positions of the shaft. For example, if there
are 8 tracks, the encoder is capable of producing 256 distinct positions or an
angular resolution of 1.406 (360/256) degrees. The most common types of
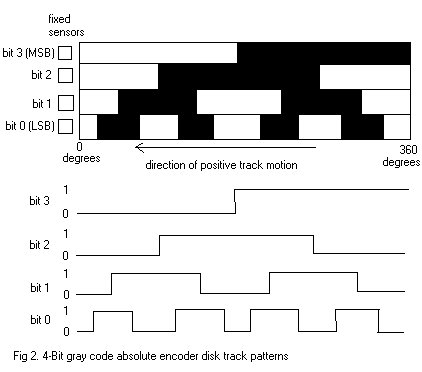
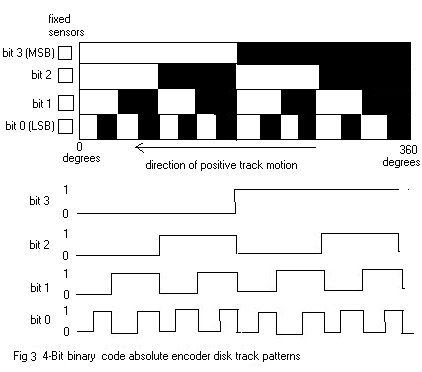
numerical encoding used in the absolute encoder are gray and binary codes. To
illustrate the acion of an absolute encoder, the gray code and natural binary
code dsisk track patterns for a simple 4-track (4-bit) encoder are illustrated
in Fig 2 and 3. The linear patterns and associated timing diagrams are what the
photodetectors sense as the code disk circular tracks rotate with the shaft. The
output bit codes for both coding schemes are listed in Table 1.
|
Decimal code |
Rotation range (deg.) |
Binary code |
Gray code |
|
0 |
0-22.5 |
0000 |
0000 |
|
1 |
22.5-45 |
0001 |
0001 |
|
2 |
45-67.5 |
0010 |
0011 |
|
3 |
67.5-90 |
0011 |
0010 |
|
4 |
90-112.5 |
0100 |
0110 |
|
5 |
112.5-135 |
0101 |
0111 |
|
6 |
135-157.5 |
0110 |
0101 |
|
7 |
15.75-180 |
0111 |
0100 |
|
8 |
180-202.5 |
1000 |
1100 |
|
9 |
202.5-225 |
1001 |
1101 |
|
10 |
225-247.5 |
1010 |
1111 |
|
11 |
247.5-270 |
1011 |
1110 |
|
12 |
270-292.5 |
1100 |
1010 |
|
13 |
292.5-315 |
1101 |
1011 |
|
14 |
315-337.5 |
1110 |
1001 |
|
15 |
337.5-360 |
1111 |
1000 |
![]() Table 1. 4-Bit gray and natural binary codes
Table 1. 4-Bit gray and natural binary codes
The gray code is designed so that only one track (one bit) will change state
for each count transition, unlike the binary code where multiple tracks (bits)
change at certain count transitions. This effect can be seen clearly in Table 1.
For the gray code, the uncertainty during a transition is only one count, unlike
with the binary code, where the uncertainty could be multiple counts.
Since the gray code provides data with the least uncertainty but the natural
binary code is the preferred choice for direct interface to computers and other
digital devices, a circuit to convert from gray to binary code is desirable.
Figure 4 shows a simple circuit that utilizes exclusive OR gates (XOR) to
perform this function.For a gray code to binary code conversion of any number of
bits N, the most signficant bits (MSB) of the binary and gray code are always
identical, and for each other bit, the binary bit is the exlcusive OR (XOR)
combination of adjacent gray code bits.
Fig 4. Gray code to binary code conversion
Incremental encoder
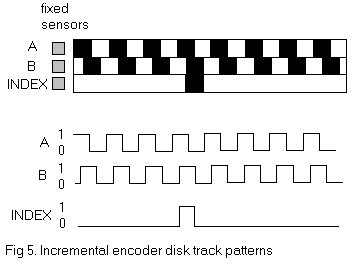 The incremental encoder,
sometimes called a relative encoder, is simpler in design than the absolute
encoder. It consists of two tracks and two sensors whose outputs are called
channels A and B. As the shaft rotates, pulse trains occur on these channels at
a frequency proportional to the shaft speed, and the phase relationship between
the signals yields the direction of rotation. The code disk pattern and output
signals A and B are illustrated in Figure 5. By counting the number of pulses
and knowing the resolution of the disk, the angular motion can be measured. The
A and B channels are used to determine the direction of rotation by assessing
which channels "leads" the other. The signals from the two channels are a 1/4
cycle out of phase with each other and are known as quadrature signals. Often a
third output channel, called INDEX, yields one pulse per revolution, which is
useful in counting full revolutions. It is also useful as a reference to define
a home base or zero position.
The incremental encoder,
sometimes called a relative encoder, is simpler in design than the absolute
encoder. It consists of two tracks and two sensors whose outputs are called
channels A and B. As the shaft rotates, pulse trains occur on these channels at
a frequency proportional to the shaft speed, and the phase relationship between
the signals yields the direction of rotation. The code disk pattern and output
signals A and B are illustrated in Figure 5. By counting the number of pulses
and knowing the resolution of the disk, the angular motion can be measured. The
A and B channels are used to determine the direction of rotation by assessing
which channels "leads" the other. The signals from the two channels are a 1/4
cycle out of phase with each other and are known as quadrature signals. Often a
third output channel, called INDEX, yields one pulse per revolution, which is
useful in counting full revolutions. It is also useful as a reference to define
a home base or zero position.
Figure 5 illustrates two separate tracks for the A and B channels, but a more
common configuration uses a single track with the A and B sensors offset a 1/4
cycle on the track to yield the same signal pattern. A single-track code disk is
simpler and cheaper to manufacture.
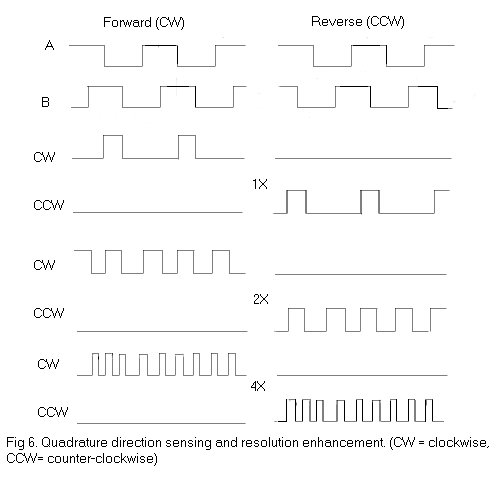
The quadrature signals A and B can be decoded to yield the direction of
rotation as hown in Figure 6. Decoding transitions of A and B by using
sequential logic circuits in different ways can provide three different
resolutions of the output pulses: 1X, 2X, 4X. 1X resolution only provides a
single pulse for each cycle in one of the signals A or B, 4X resolution provides
a pulse at every edge transition in the two signals A and B providing four times
the 1X resolution. The direction of rotation(clockwise or counter-clockwise) is
determined by the level of one signal during an edge transition of the second
signal. For example, in the 1X mode, A=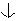 with B =1 implies a clockwise pulse, and B=
with B =1 implies a clockwise pulse, and B=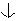 with A=1 implies a
counter-clockwise pulse. If we only had a single output channel A or B, it would
be impossible to determine the direction of rotation. Furthermore, shaft jitter
around an edge transition in the single signal woudl result in erroneous
pulses..
with A=1 implies a
counter-clockwise pulse. If we only had a single output channel A or B, it would
be impossible to determine the direction of rotation. Furthermore, shaft jitter
around an edge transition in the single signal woudl result in erroneous
pulses..
(Materials taken from Introduction to Mechatronics and Measurement
Systems, Histand & Alciatore, 1999 McGraw Hill)
 A digital optical encoder is a
device that converts motion into a sequence of digital pulses. By counting a
single bit or by decoding a set of bits, the pulses can be converted to relative
or absolute position measurements. Encoders have both linear and rotary
configurations, but the most common type is rotary. Rotary encoders are
manufactured in two basic forms: the absolute encoder where a unique digital
word corresponds to each rotational position of the shaft, and the incremental
encoder, which produces digital pulses as the shaft rotates, allowing
measurement of relative position of shaft. Most rotary encoders are composed of
a glass or plastic code disk with a photographically deposited radial pattern
organized in tracks. As radial lines in each track interrupt the beam between a
photoemitter-detector pair, digital pulses are produced.
A digital optical encoder is a
device that converts motion into a sequence of digital pulses. By counting a
single bit or by decoding a set of bits, the pulses can be converted to relative
or absolute position measurements. Encoders have both linear and rotary
configurations, but the most common type is rotary. Rotary encoders are
manufactured in two basic forms: the absolute encoder where a unique digital
word corresponds to each rotational position of the shaft, and the incremental
encoder, which produces digital pulses as the shaft rotates, allowing
measurement of relative position of shaft. Most rotary encoders are composed of
a glass or plastic code disk with a photographically deposited radial pattern
organized in tracks. As radial lines in each track interrupt the beam between a
photoemitter-detector pair, digital pulses are produced.

 The incremental encoder,
sometimes called a relative encoder, is simpler in design than the absolute
encoder. It consists of two tracks and two sensors whose outputs are called
channels A and B. As the shaft rotates, pulse trains occur on these channels at
a frequency proportional to the shaft speed, and the phase relationship between
the signals yields the direction of rotation. The code disk pattern and output
signals A and B are illustrated in Figure 5. By counting the number of pulses
and knowing the resolution of the disk, the angular motion can be measured. The
A and B channels are used to determine the direction of rotation by assessing
which channels "leads" the other. The signals from the two channels are a 1/4
cycle out of phase with each other and are known as quadrature signals. Often a
third output channel, called INDEX, yields one pulse per revolution, which is
useful in counting full revolutions. It is also useful as a reference to define
a home base or zero position.
The incremental encoder,
sometimes called a relative encoder, is simpler in design than the absolute
encoder. It consists of two tracks and two sensors whose outputs are called
channels A and B. As the shaft rotates, pulse trains occur on these channels at
a frequency proportional to the shaft speed, and the phase relationship between
the signals yields the direction of rotation. The code disk pattern and output
signals A and B are illustrated in Figure 5. By counting the number of pulses
and knowing the resolution of the disk, the angular motion can be measured. The
A and B channels are used to determine the direction of rotation by assessing
which channels "leads" the other. The signals from the two channels are a 1/4
cycle out of phase with each other and are known as quadrature signals. Often a
third output channel, called INDEX, yields one pulse per revolution, which is
useful in counting full revolutions. It is also useful as a reference to define
a home base or zero position.